TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

 

EM TODAS AS ÁREAS DA FÍSICIA E EM SEUS FENÔMENOS EM ESCALA ÍNFIMA E INFINITA, E EM TERMOS DO INFINITO-DIMENSIONAL GRACELI, SE TEM UM UNIVERSO DE INDETERMINALIDADE E ALEATORIEDADE, NÃO VOU TRATAR COMO QUÂNTICO POR SE TRATAR NESTE CASO DE TEORIA DE ONDAS.

OU SEJA, SE TEM UM FERRO EM INCANDESCÊNCIA SE TEM NESTE CASO AS PARTÍCULAS DO FERRO COM VARIAÇÕES DE PROCESSOS E TRANSFORMAÇÕES ÍNFIMAS DENTRO DO SISTEMA DO INFINITO DIMENSIONAL GRACELI.

OU SEJA, SE ENCONTRA NUM UNIVERSO DE INDETERMINALIDADE E ALEATORIEDADE DINÃMICA E TRANSFORMATIVA.

COM PROCESSOS E INTENSIDADES ESPECÍFICOS PARA O FERRO.

OU SEJA, SE TEM 

 TEORIA GENERALIZADA GRACELI DA ABSORÇÃO, EMISSSÃO, TRANSIÇÃO, TRANSFERÊNCIA DE ENERGIA E MOMENTUN, TUNELAMENTO, DIFUSÃO, REFRAÇÃO, RETRAÇÃO, FUSÕES, DILATAÇÃO,  E OUTROS.

E  PONTOS CRÍTICOS DE FUSÕES, EBULIÇÕES, MUDANÇAS DE FASES, ENTROPIAS, ENTALPIAS, ETC.

ACELERAÇÕES DE FENÔMENOS TERMICOS, RADIAÇÕES, E DILATAÇÕES., ETC.

ISTO PARA TODOS OS FENÔMENSO DENTRO DAS FÍSICAS E QUÍMICAS.

SENDO QUE CADA UM DESTES FENÔMENOS CONTÉM RELAÇÕES ENTRE SI E CONFORME OS TIPOS DE MATERIAIS E MESMO NUM MESMO TIPO DE  MATERIAL VARIA DE UNS PARA OUTROS, .

EXEMPLO.

COMO DE FERRO PARA ALUMÍNIO, E DE ALGUNS ALUMÍNIOS PARA OUTROS ALUMÍNIOS,

O MESMO PARA TODOS OS TIPOS DE MATERIAIS E ELEMENTOS QUÍMICO, MOLÍCULAS E PARTÍCULAS.

E CONORME O SISTEMA DO INFINITO-DIMENSIONAL GRACELI.

OU SEJA, UM RELATIVISMO QUÍMICO E FÍSICO QUÍMICO.

 RELATIVIDADE DIMENSIONAL GRACELI.

 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

outubro 27, 2021

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.

NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.

JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químico

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

Na análise de transferência de calor, difusividade térmica é a condutividade térmica dividida por densidade e capacidade específica de calor a pressão constante.^[1] Mede a taxa de transferência de calor de um material do lado quente para o lado frio. Ele tem a unidade derivada SI de m² / s. A difusividade térmica é geralmente denotada ${\displaystyle \alpha }$, mas ${\displaystyle a}$, ${\displaystyle \kappa }$^[2], ${\displaystyle K}$,^[3] e ${\displaystyle D}$ também são usados. A fórmula é:

${\displaystyle \alpha ={k \over {\rho \,c_{p}}},}$^[4]

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde:

• ${\displaystyle k}$ é condutividade termal (W/(m·K))
• ${\displaystyle \rho }$ é densidade (kg/m³)
• ${\displaystyle c_{p}}$ é capacidade de calor específica (J/(kg·K))

Juntos, ${\displaystyle (\rho \,c_{p})}$ podem ser considerados a capacidade de calor volumétrico (J/(m³·K)).

Como visto na equação do calor,^[5]

${\displaystyle {\frac {\partial T}{\partial t}}=\alpha \nabla ^{2}T}$,

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

uma maneira de visualizar a difusividade térmica é como a razão entre tempo derivado de temperatura e sua curvatura, quantificando a taxa na qual a concavidade da temperatura é "suavizada Fora". Em certo sentido, a difusividade térmica é a medida da inércia térmica.^[6] Em uma substância com alta difusividade térmica, o calor se move rapidamente através dela porque a substância conduz calor rapidamente em relação à sua capacidade volumétrica de calor ("thermal bulk").

Anel de Gravesande, usado para descrever o fenômeno de expansão térmica.

Dilatação térmica é o aumento das dimensões de um corpo ocasionado pelo aumento de sua temperatura, o que causa o aumento no grau de agitação de suas moléculas e consequentemente aumento na distância média entre as mesmas. A dilatação ocorre de forma mais significativa nos gases, de forma intermediária nos líquidos e de forma menos explícita nos sólidos, podendo-se afirmar que:

Dilatação nos gases > Dilatação nos líquidos > Dilatação nos sólidos.

Experimentos podem ser usados para mostrar a dilatação de forma mais evidente, como o identificado na figura, que consiste de uma esfera, um anel, uma haste e uma vela. A esfera, quando em temperatura ambiente, passa facilmente pelo orifício, quando aquecemos a mesma, ela sofre expansão térmica, não passando mais pelo anel. Podemos chegar ao mesmo resultado, mantendo a temperatura da esfera e resfriando o anel, que por sua vez comprime, impossibilitando a passagem da esfera.

Índice

• 1Coeficiente de dilatação térmica '"`UNIQ--postMath-00000001-QINU`"'
  • 1.1Equação genérica: materiais isotrópicos
  • 1.2Tensor de dilatação térmica: materiais anisotrópicos
• 2Tipos de Dilatação
  • 2.1Dilatação linear
    • 2.1.1Dilatação do vazio
  • 2.2Dilatação superficial
  • 2.3Dilatação volumétrica
    • 2.3.1Dilatação Anômala da Água
• 3Coeficientes de dilatação linear
• 4Ver também
• 5Referências

Coeficiente de dilatação térmica ${\displaystyle \alpha }$

Equação genérica: materiais isotrópicos

Nos materiais isotrópicos pode-se calcular a variação de comprimento, e consequentemente de área e volume, em função da variação de temperatura:

${\displaystyle \Delta L=\alpha \cdot L_{0}\cdot \Delta T}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

• ${\displaystyle \Delta L:\ }$variação do comprimento;
• ${\displaystyle \alpha :\ }$coeficiente de dilatação linear;
• ${\displaystyle L_{0}:\ }$comprimento inicial;
• ${\displaystyle \Delta T=T-T_{0}:\ }$
  /////

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

  variação de temperatura.

Tensor de dilatação térmica: materiais anisotrópicos

Os materiais cristalinos não cúbicos apresentam uma dilatação anisotrópica:o seu coeficiente de dilatação ${\displaystyle \alpha \,}$ varia com a direção. Para descrever a sua dilatação recorre-se a um tensor simétrico de ordem 2:

${\displaystyle {\begin{bmatrix}\alpha _{11}&\alpha _{12}&\alpha _{13}\\\alpha _{21}=\alpha _{12}&\alpha _{22}&\alpha _{23}\\\alpha _{31}=\alpha _{13}&\alpha _{32}=\alpha _{23}&\alpha _{33}\end{bmatrix}}}$

Por exemplo, para uma rede triclínica é necessário conhecer seis coeficientes de dilatação ortogonais, que não têm necessariamente que coincidir com os eixos do cristal.

Os valores próprios do tensor de dilatação térmica ou coeficientes de dilatação linear principais ${\displaystyle \alpha _{1}\,}$, ${\displaystyle \alpha _{2}\,}$ e ${\displaystyle \alpha _{3}\,}$, permitem obter o coeficiente de dilatação volúmica traço do tensor: ${\displaystyle \beta =\alpha _{1}+\alpha _{2}+\alpha _{3}=\alpha _{11}+\alpha _{22}+\alpha _{33}\,}$

Tipos de Dilatação

Quanto à dilatação dos corpos, esta é de três tipos.

Dilatação linear

Na dilatação linear (uma dimensão), considera-se uma das dimensões do sólido: o comprimento. Uma barra aumenta linearmente. As barras dos trilhos ferroviários são feitas com um espaçamento para a dilatação não envergarem com ganho de calor, ou retraírem com a queda da temperatura. Vale lembrar também que a dilatação não é um fenômeno visível, variando de acordo com o material e a temperatura. A dilatação linear é apenas teórica, sendo que para que algo exista este deve ser tridimensional. A matéria dilata-se em três dimensões, mas como não é possível calcular essa dilatação, adota-se somente o calculo da dilatação linear. O coeficiente de dilatação linear (${\displaystyle \alpha }$) é constante em apenas alguns intervalos de temperaturas, por isso seus valores tabelados são obtidos por médias de temperaturas.

Trilhos de trem envergados por dilatação térmica.^[1]

${\displaystyle \Delta L=\alpha \cdot L_{0}\cdot \Delta T,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 onde:

• ${\displaystyle \Delta L}$ é a variação do comprimento do corpo que sofreu a dilatação linear em metros (${\displaystyle m}$);
• ${\displaystyle \alpha }$ é o coeficiente de dilatação linear do material que constitui o corpo em grau Celsius recíproco (${\displaystyle ^{\circ }C^{-1}}$);
• ${\displaystyle L_{0}}$ é o comprimento inicial da superfície do corpo em metros (${\displaystyle m}$);
• ${\displaystyle \Delta T}$ é a variação de temperatura sofrida pelo corpo em grau Celsius (${\displaystyle ^{\circ }C}$).

Dilatação do vazio

Para avaliar o comportamento de uma chapa metálica com um orifício no centro, podemos avaliar o sistema separadamente, pensando que os objetos são formados por moléculas, e quando aquecidas, estas se agitam, aumentando a distância de uma para as outras. Logo, as moléculas da borda do furo devem obedecer a este princípio, como a única maneira disso ocorrer é no sentido da placa, o perímetro do círculo acaba aumentando. Basicamente é conveniente saber que o espaço vazio sofre expansão da mesma forma que sofreria se estivesse preenchido.^[2]

Dilatação superficial

Na dilatação superficial (superfície = área, logo, neste caso temos duas dimensões). A dilatação do comprimento e da largura de uma chapa de aço é superficial. Se um disco ou chapa com um furo central dilatar, o tamanho do furo e da chapa aumentam simultaneamente. Ou seja, é aquela em que predomina a variação em duas dimensões, isto é, a variação da área.

${\displaystyle \Delta S=\beta \cdot S_{0}\cdot \Delta T}$, 

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde:

• ${\displaystyle \Delta S}$ é a variação da área superficial do corpo que sofreu a dilatação linear em metros quadrados (${\displaystyle m^{2}}$);
• ${\displaystyle \beta }$ é o coeficiente de dilatação superficial do material que constitui o corpo em grau Celsius recíproco (${\displaystyle ^{\circ }C^{-1}}$). É importante destacar que ${\displaystyle \beta =2\alpha }$
• ${\displaystyle S_{0}}$ é a área inicial da superfície do corpo em metros quadrados (${\displaystyle m^{2}}$);
• ${\displaystyle \Delta T}$ é a variação de temperatura sofrida pelo corpo em grau Celsius (${\displaystyle ^{\circ }C}$).

Dilatação volumétrica

Na dilatação volumétrica calcula-se a variação do volume, logo, avaliamos três dimensões. A dilatação de um líquido ou de um gás é volumétrica. O coeficiente de dilatação volumétrica (${\displaystyle \gamma }$) é dado da seguinte forma: Coeficiente de dilatação linear multiplicado por três, tal procedimento é explicado pelo fato de que quando calculamos um volume levamos em conta as três dimensões (altura, largura e comprimento).

${\displaystyle \Delta V=\gamma \cdot V_{0}\cdot \Delta T}$, 

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde:

• ${\displaystyle \Delta V}$ é a variação do volume do corpo que sofreu a dilatação linear em metros cúbicos (${\displaystyle m^{3}}$);
• ${\displaystyle \gamma }$ é o coeficiente de dilatação volumétrico do material que constitui o corpo em grau Celsius recíproco (${\displaystyle ^{\circ }C^{-1}}$). É importante salientar que ${\displaystyle \gamma =3\alpha }$;
• ${\displaystyle V_{0}}$ é o volume inicial da superfície do corpo em metros cúbicos (${\displaystyle m^{3}}$);
• ${\displaystyle \Delta T}$ é a variação de temperatura sofrida pelo corpo em grau Celsius (${\displaystyle ^{\circ }C}$).

Dilatação Anômala da Água

• A dilatação da água apresenta uma anomalia em relação as outras substâncias, tendo seu volume diminuído quando alcança a temperatura de 4 °C (à pressão normal).

(fato mostrado na curva contida no gráfico Volume por Temperatura.).

Olhando para o lado ecológico, nos perguntamos como espécies aquáticas sobrevivem ao alto inverno. A explicação está relacionada com a anomalia térmica da água. Quando a temperatura baixa, a densidade aumenta, fazendo com que a água quente suba e a mais fria desça, originando correntes para cima e para baixo. Quando a temperatura de toda água presente no sistema chega a 4 °C, o fluxo das correntes para, fazendo com que a água do fundo não suba e a da margem não desça. Isto ocorre, pois a esta temperatura, a densidade da água é máxima. O inverno vai ficando mais rigoroso e a superfície da água se congela, porém abaixo desta camada a água continua em estado líquido. O gelo é um bom isolante térmico (mau condutor), portanto essa camada isola a água líquida inferior do meio externo, impedindo o congelamento de toda água. Isto possibilita que a vida das espécies aquáticas continue durante os períodos mais frios.A densidade da água aumenta entre 0 °C a 4 °C, seguindo da diminuição da densidade a partir de 4 °C.^[3]

Coeficientes de dilatação linear

Os coeficientes de dilatação linear de algumas substâncias e elementos químicos^[4][5] a seguir indicados aplicam-se à faixa de temperaturas indicada. Quando não indicada presume-se uma temperatura ambiente. Na realidade estes coeficientes variam com a temperatura mas assume-se a sua exatidão na faixa mostrada.

Nota: clicando em cada um dos títulos é possível reordenar a tabela.

Substância α 10^-6(máx.) α 10^-6(min.) Faixa de temperaturas Gálio 120,0 vgv Índio 32,1 Zinco e suas ligas 35,0 19,0 100 °C-390 °C Chumbo e suas ligas 29,0 26,0 100 °C-390 °C Alumínio e suas ligas 25,0 21,0 100 °C-390 °C Latão 18,0 21,0 100 °C-390 °C Prata 20,0 100 °C-390 °C Aço inoxidável 19,0 11,0 540 °C-980 °C Cobre 18,0 14,0 100 °C-390 °C Níquel e suas ligas 17,0 12,0 540 °C-980 °C Ouro 14,0 100 °C-390 °C Aço 14,0 10,0 540 °C-980 °C Cimento (concreto)[6] 6,8 11,9 Temp. ambiente Platina 9,0 100 °C-390 °C Vidro (de janela)[7] 8,6 20 °C-300 °C Cromo 4,9 Tungstênio 4,5 Temp. ambiente Vidro borossilicato (vidro pyrex)[8] 3,2 20 °C-300 °C Carbono e Grafite 3,0 2,0 100 °C-390 °C Silício 2,6 Quartzo fundido [9] 0,55

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Em termodinâmica, o efeito Joule-Thomson ou efeito Joule-Kelvin ou efeito Kelvin-Joule descreve a variação da temperatura de um gás ou líquido quando ele é forçado a passar através de uma válvula ou tampão poroso, enquanto mantido isolado, de modo que nenhum calor seja trocado com o ambiente.^[1][2][3] Este procedimento é chamado de processo de estrangulamento ou válvula Joule-Thomson.^[4] À temperatura ambiente, todos os gases, exceto hidrogênio, hélio e neônio, resfriam-se sob a expansão do experimento de Joule-Thomson.^[5][6]

O efeito tem esse nome em homenagem a James Prescott Joule e William Thomson, o 1º Barão Kelvin, que descobriram-no em 1852, na sequência de trabalhos anteriores de Joule sobre a expansão de Joule, em que um gás sofre expansão livre no vácuo.

Índice

• 1Descrição
• 2O mecanismo físico
• 3O coeficiente de Joule-Thomson
• 4Aplicações
• 5Demonstração de que a entalpia permanece constante em um processo de Joule-Thomson
• 6Dedução do coeficiente de Joule–Thomson
• 7Ver também
• 8Referências
• 9Bibliografia
• 10Ligações externas

Descrição

A expansão adiabática (sem troca de calor) de um gás pode ser realizada de várias maneiras. A mudança de temperatura experimentada pelo gás durante a expansão depende não só das pressões inicial e final, mas também da maneira como a expansão é realizada.

• Se o processo de expansão é reversível, o que significa que o gás está em equilíbrio termodinâmico em todos os instantes, ela é chamada expansão isentrópica. Neste cenário, o gás realiza trabalho positivo durante a expansão, e sua temperatura diminui.
• Em uma expansão livre, por outro lado, o gás não realiza trabalho e não absorve calor, assim a energia interna é conservada. Expandido livremente, a temperatura de um gás ideal deveria permanecer constante, mas a temperatura de um gás real pode aumentar ou diminuir, dependendo da temperatura e pressão iniciais.
• O método de expansão discutido neste artigo, no qual um gás ou líquido a uma pressão P1 flui para uma região à baixa pressão P2 através de uma válvula ou tampão poroso, sob condições estáveis e sem variação na energia cinética, é chamada de experimento de Joule-Thomson . Durante este processo, a entalpia permanece inalterada (veja a demostração abaixo).

O processo de estrangulamento ocorre ao longo de uma curva à entalpia constante, no sentido em que a pressão diminui, o que significa que o processo ocorre da esquerda para a direita em um diagrama T-P. À medida que avançamos ao longo de uma curva de entalpia constante, a altas pressões, a temperatura aumenta, até a temperatura de inversão. Então, como o líquido continua a se expandir, a temperatura cai. Se fizermos isso para várias curvas de entalpia constante e juntarmos os pontos de inversão, uma curva chamada de curva de inversão é obtida. Esta curva intercepta o eixo T em alguma temperatura, chamada de temperatura de inversão máxima. Para o hidrogênio, a temperatura é -68°. Na refrigeração por compressão de vapor, é preciso regular a pressão do gás e resfriá-lo ao mesmo tempo. Isto representa uma barreira para as substâncias cuja temperatura de inversão máxima está bem abaixo da temperatura ambiente. Assim, o hidrogênio precisa ser resfriado abaixo de sua temperatura de inversão se o resfriamento é obtido através do estrangulamento.

O mecanismo físico

Uma vez que o gás se expande, a distância média entre as moléculas aumenta. Devido às forças atrativas intermoleculares (ver força de van der Waals), a expansão produz um aumento na energia potencial do gás. Se nenhum trabalho externo é extraído no processo e nenhum calor é transferido, a energia total do gás permanece a mesma por causa da conservação da energia. O aumento da energia potencial, portanto, implica numa diminuição da energia cinética e portanto uma diminuição de temperatura.

Um segundo mecanismo tem o efeito oposto. Durante as colisões com as moléculas do gás, a energia cinética é temporariamente convertida em energia potencial. Como a distância média intermolecular aumenta, há uma queda no número de colisões por unidade de tempo, o que provoca uma diminuição da energia potencial média. Mais uma vez, a energia total é conservada, então isto leva a um aumento na energia cinética (temperatura). Abaixo da temperatura de inversão de Joule-Thomson, o efeito anterior (o trabalho interno realizado contra as forças atrativas intermoleculares) predomina, e a expansão livre provoca uma diminuição na temperatura. Acima da temperatura de inversão, as moléculas de gás se movem mais rapidamente e assim colidem com mais freqüência, e o último efeito (colisões reduzidas produzindo diminuição na energia potencial média) predomina: a expansão de Joule-Thomson provoca um aumento da temperatura.

O coeficiente de Joule-Thomson

Coeficientes de Joule-Thomson para vários gases à pressão atmosférica.

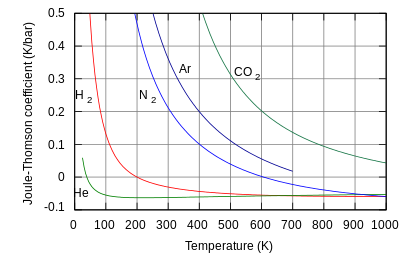
A taxa de variação da temperatura T em relação à pressão P em um processo de Joule-Thomson (isto é, à entalpia constante H) é o coeficiente de Joule-Thomson ${\displaystyle \mu _{\mathrm {JT} }}$. Este coeficiente pode ser expresso em termos do volume V do gás, da sua capacidade térmica à pressão constante ${\displaystyle C_{\mathrm {p} }}$ e de seu coeficiente de expansão térmica ${\displaystyle \alpha }$ como:^[1][3][7]

${\displaystyle \mu _{\mathrm {JT} }\equiv \left({\partial T \over \partial P}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}\left(\alpha T-1\right)\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Veja a dedução do coeficiente de Joule-Thomson (Kelvin) abaixo, para a demonstração desta relação. O valor de ${\displaystyle \mu _{\mathrm {JT} }}$ é normalmente expresso em °C/bar (SI units: K/Pa) e depende do tipo de gás, da temperatura e da pressão do gás antes da expansão. A sua dependência com a pressão normalmente é apenas uma pequena percentagem para pressões até 100 bar.

Todos os gases reais têm um ponto de inversão no qual o valor de ${\displaystyle \mu _{\mathrm {JT} }}$ muda de sinal. A temperatura ndeste ponto, a temperatura de inversão de Joule-Thomson, depende da pressão do gás antes da expansão.

Numa expansão a pressão diminui, assim o sinal de ${\displaystyle \partial P}$ é negativo por definição. Com isso em mente, a tabela a seguir mostra quando o efeito Joule-Thomson resfria ou aquece um gás real:

Se a temperatura do gás está	então ${\displaystyle \mu _{\mathrm {JT} }}$ é	desde que ${\displaystyle \partial P}$ é	assim ${\displaystyle \partial T}$ deve ser	logo o gás
abaixo da temperatura de inversão	positivo	sempre negativo	negativo	é resfriado
acima da temperatura de inversão	negativo	sempre negativo	positivo	é aquecido

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Hélio e hidrogênio são dois gases cujas temperaturas de inversão de Joule-Thomson a uma pressão de 1 atm são muito baixas (por exemplo, cerca de 51 K (-222 °C) para o hélio). Assim, o hélio e o hidrogênio aquecem-se quando expandem-se à entalpia constante à temperatura ambiente típica. Por outro lado, o nitrogênio e o oxigênio, os dois gases mais abundantes na atmosfera, têm temperaturas inversão de 621 K (348 °C) e 764 K (491 °C), respectivamente: estes gases podem ser resfriados à temperatura ambiente pelo efeito Joule-Thomson.^[1]

Para um gás ideal, ${\displaystyle \mu _{\mathrm {JT} }}$ é sempre igual a zero: gases ideais nem se aquecem nem se resfriam ao serem expandidos à entalpia constante.

Aplicações

Na prática, o efeito Joule-Thomson é realizado permitindo-se que o gás se expanda através de um dispositivo de estrangulamento (normalmente uma válvula), que deve estar muito bem isolado para impedir qualquer transferência de calor para ou pelo gás. Nenhum trabalho externo é extraído do gás durante a expansão (o gás não deve ser expandido através de uma turbina, por exemplo).

O efeito é aplicado com a técnica de Linde como um processo padrão na indústria petroquímica, onde a refrigeração é utilizada para liquefazer gases, e também em várias aplicações criogênicas (por exemplo, para a produção de oxigênio, nitrogênio, e argônio líquidos). Apenas quando o coeficiente de Joule-Thomson para o gás na determinada temperatura é maior que zero o gás pode ser liquefeito a essa temperatura pelo ciclo de Linde. Em outras palavras, um gás deve estar abaixo da sua temperatura de inversão para ser liquefeito pelo ciclo de Linde. Por esta razão, o ciclo de Linde simples normalmente não pode ser utilizado para liquefazer hélio, hidrogênio e neônio.

Demonstração de que a entalpia permanece constante em um processo de Joule-Thomson

Em um processo de Joule-Thomson a entalpia permanece constante. Para demonstrar isso, o primeiro passo é calcular o trabalho líquido realizado pelo gás que se move através da válvula. Suponha que o gás tem um volume V₁ na região à pressão P₁ (região 1) e um volume V₂ quando ele chega à região à pressão P₂ (região 2). Então o trabalho realizado sobre o gás pela fração de gás na região 1 é P₁V₁. Na região 2, o trabalho realizado pelo gás é P₂V₂. Assim, o trabalho total realizado pelo gás é

${\displaystyle P_{2}V_{2}-P_{1}V_{1}\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A variação na energia interna mais o trabalho realizado pelo gás é, pela primeira lei da termodinâmica, a quantidade total de calor absorvido pelo gás (aqui supõe-se que não há variação na energia cinética). No processo de Joule-Thomson, o gás é mantido isolado, de forma que nenhum calor é absorvido. Isso significa que

${\displaystyle U_{2}-U_{1}+P_{2}V_{2}-P_{1}V_{1}=0\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle U_{1}}$ e ${\displaystyle U_{2}}$ denotam a energia interna do gás nas regiões 1 e 2, respectivamente.

Utilizando a definição de entalpia ${\displaystyle H=U+PV}$, 

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

a equação acima implica que:

${\displaystyle H_{1}=H_{2}\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle H_{1}}$ e ${\displaystyle H_{2}}$ denotam a entalpia do gás nas regiões 1 e 2, respectivamente.

Dedução do coeficiente de Joule–Thomson

É uma dedução da expressão

${\displaystyle \mu _{\mathrm {JT} }\equiv \left({\frac {\partial T}{\partial P}}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}\left(\alpha T-1\right)\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

para o coeficiente de Joule–Thomson.

A derivada parcial de T em relação a P a H constante pode ser calculada expressando-se a entalpia diferencial dH em termos de dT e dP, e igualando-se a expressão resultante a zero e resolvendo-se para a razão entre dT e dP.

Segue da relação termodinâmica fundamental que a diferencial da entalpia e dada por:

${\displaystyle dH=TdS+VdP\,}$ (aqui ${\displaystyle S}$ é a entropia do gás).

Expressando dS em termos de dT e dP, temos:

${\displaystyle dH=T\left({\frac {\partial S}{\partial T}}\right)_{P}dT+\left[V+T\left({\frac {\partial S}{\partial P}}\right)_{T}\right]dP\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Usando

${\displaystyle C_{\mathrm {p} }=T\left({\frac {\partial S}{\partial T}}\right)_{P}\,}$ 

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

(ver Calor específico), podemos escrever:

${\displaystyle dH=C_{\mathrm {p} }dT+\left[V+T\left({\frac {\partial S}{\partial P}}\right)_{T}\right]dP\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A derivada parcial de S restante pode ser expressa em termos do coeficiente de expansão térmica através de uma relação de Maxwell, como se segue. A partir da relação termodinâmica fundamental, segue-se que a diferencial da energia de Gibbs é dada por:

${\displaystyle dG=-SdT+VdP\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A simetria entre as derivadas parciais de G em relação a T e P implica que:

${\displaystyle \left({\frac {\partial S}{\partial P}}\right)_{T}=-\left({\frac {\partial V}{\partial T}}\right)_{P}=-V\alpha \,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle \alpha }$ é o coeficiente de expansão térmica. Usando esta relação, a diferencial de H pode ser expressa como

${\displaystyle dH=C_{\mathrm {p} }dT+V\left(1-T\alpha \right)dP\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Igualando dH a zero e resolvendo para dT/dP, obtemos finalmente:

${\displaystyle \left({\frac {\partial T}{\partial P}}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}\left(\alpha T-1\right)\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

É fácil verificar que para um gás ideal o coeficiente de expansão térmica ${\displaystyle \alpha }$ é ${\displaystyle 1/T}$, e assim um gás ideal não sente o efeito Joule-Thomson. O resfriamento de um gás por uma expansão isentrópica pura não é o resfriamento de Joule-Thomson, embora isso seja às vezes erroneamente chamado de resfriamento Joule-Thomson por alguns profissionais experimentais.

O efeito Unruh, descoberto em 1976 por Bill Unruh da Universidade da Colúmbia Britânica, é a predição de que um observador acelerado vai perceber radiação de buracos negros enquanto um outro observador em repouso inercial não irá observar nenhum. Em outras palavras, o observador acelerado vai se encontrar em um ambiente mais aquecido. O estado quântico que é visto como um estado estático pelo observador inercial, é visto como um equilíbrio termodinâmico pelo observador uniformemente acelerado.

Índice

• 1Teoria
• 2Temperatura Unruh
• 3Referências
• 4Ligações externas

Teoria

Unruh demonstrou que mesmo a noção de vácuo depende do caminho que o observador percorre pelo espaço-tempo. Do ponto de vista do observador acelerado, o vácuo do observador inercial vai se assemelhar a um estado contendo várias partículas em um equilíbrio térmico – um gás aquecido. Apesar do Efeito Unruh parecer não intuitivo, faz perfeito sentido se a idéia de vácuo for corretamente interpretada.

Na física moderna o conceito de vácuo não é o mesmo que "espaço-vazio", como tudo mais no espaço é preenchido por campos quânticos que formam o universo. O vácuo é simplesmente o menor estado de energia possível deste campo.

Segundo a teoria da relatividade restrita, dois observadores se movendo relativamente em sentidos opostos devem utilizar diferentes coordenadas de tempo. Se estes observadores estiverem acelerados eles também deverão utilizar diferentes coordenadas espaciais. Cada um dos observadores irá enxergar diferentes estados quânticos e diferentes vácuos.

Em alguns casos, o vácuo de um observador não é sequer no espaço do espaço quântico do outro observador. Em termos técnicos, isto é por causa dos dois vácuos levarem a representações completamente diferentes do campo quântico.

A existência da radiação de Unruh pode ser referenciada para o horizonte de eventos, colocando-se no mesmo esboço conceitual da radiação Hawking. Por outro lado, o efeito Unruh mostra que a definição do que constitui uma partícula depende do estado inercial do observador.

Temperatura Unruh

A temperatura de Unruh é a temperatura efetiva experimentada por um detector uniformemente acelerado em um campo de vácuo, dada por:^[1]

${\displaystyle T={\frac {\hbar a}{2\pi ck_{\mathrm {B} }}},}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ħ é a constante de Planck reduzida, a é a aceleração local, c é a velocidade da luz, e k_B é a constante de Boltzmann. Dessa forma, por exemplo, uma aceleração própria de 2.47×10²⁰ m·s^-2 corresponde aproximadamente a uma temperatura de 1 K. Inversamente, uma aceleração de 1 m·s^-2 corresponde a uma temperatura de 4.06×10⁻²¹ K.

A temperatura de Unruh tem a mesma forma da temperatura de Hawking T_H = ħg2πck_B 

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

para um buraco negro. Tal expressão foi obtida por Stephen Hawking de maneira independente por volta da mesma época. Por isso, tais equações são referenciadas também como Temperatura de Hawking–Unruh.^[2]

A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação E_F, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi.

Índice

• 1Introdução
  • 1.1Contexto geral
  • 1.2Contexto avançado
• 2Ilustração do conceito para compartimento monodimensional quadrado
• 3O caso tridimensional
• 4Energias de Fermi típicas
  • 4.1Anãs brancas
  • 4.2Núcleos
• 5Referências
• 6Bibliografia
• 7Ver também

Introdução

Contexto geral

A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos.

A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral.

Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres.

Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos.

A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação:

${\displaystyle \mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ε_F é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, ε_F/k. Esta temperatura característica é da ordem de 10⁵K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac.

Contexto avançado

Principais energias em estrutura de bandas para sólidos cristalinos.

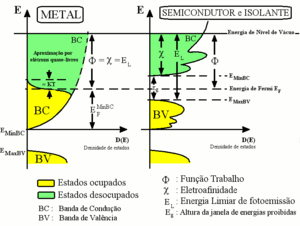
Elétrons são férmions, ou seja, são partículas regidas pela estatística de Fermi. Nesta estatística, um dado estado quântico pode ser ocupado por no máximo um e não mais que um férmion, e portanto a máxima probabilidade de ocupação de um dado estado quântico é um. Os elétrons situados dentro da amostra estão confinados por um potencial atrativo exercido pelos íons positivos da rede. Conforme mostrado pela mecânica quântica, potenciais confinantes apresentam níveis de energias discretos. No caso dos átomos isto se reflete nos tão conhecidos níveis atômicos de energia e no caso dos sólidos cristalinos, a aproximação entre os átomos leva a um agrupamento dos estados em bandas de energia. Estas bandas são vistas nas relações de dispersão para os sólidos como sendo as regiões de energia permitidas para os elétrons, separadas umas das outras por janelas de energias proibidas (ou “gaps”).

Rigorosamente falando,^[1] a energia do nível de Fermi é definida em sistemas à temperatura de zero absoluto. Nesse caso, a energia do nível de Fermi é a energia do nível mais energético ocupado, visto que nessa temperatura todos os níveis com energia menor que a energia do nível de Fermi estariam ocupados (probabilidade igual a 1) e todos os níveis com energia acima, desocupados (probabilidade de ocupação nula). Para sistemas em temperaturas não nulas, não temos mais uma transição abrupta da probabilidade de ocupação, e sim uma probabilidade dada pela distribuição de Fermi-Dirac. Considera-se então como a energia do nível de Fermi a energia obtida pela média aritmética ponderada das energias de cada estado energético afetado pela excitação térmica (estados com probabilidades de ocupação diferentes de 1 ou 0) pesadas cada qual pela respectiva probabilidade de ocupação do estado associado. O denominador desta média será obviamente o número de estados envolvidos no processo. Repare que em acordo com a estatística de Fermi, dentre os referidos estados os menos energéticos têm probabilidade de ocupação maior do que aqueles mais energéticos. Para aproximação de elétrons livres a densidade de estados cresce com a raiz quadrada da energia, resultando em uma parábola no gráfico de energia x densidade de estados. Em semicondutores e isolantes esta dependência pode ser bem mais complicada.

Outra definição equivalente implica dizer que a energia de Fermi corresponde ao potencial eletroquímico do sistema na temperatura de zero absoluto. Uma extensão a temperaturas maiores é evidente, e a energia de Fermi corresponde assim ao potencial eletroquímico do sistema na temperatura considerada. A energia de Fermi expressa, portanto, qual seria a variação da energia interna total do sólido, considerado sempre como sistema isolado e em equilíbrio termodinâmico, caso um elétron fosse dele removido. Sendo E_N^total a energia total do sistema no estado neutro, em seu equilíbrio termodinâmico, e E_N-1^total a energia total do sistema também em seu novo equilíbrio termodinâmico mas após a remoção do elétron, temos que:

E_F = E_N^total - E_N-1^total

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Nas definições acima, o nível de referência é o nível de menor energia disponível aos N elétrons, e a remoção de um elétron provoca, então, a redução da energia do sistema. Neste referencial a energia de Fermi é, portanto, positiva, bem como o potencial eletroquímico.

Quando dois materiais diferentes são colocados em contato, a condição de equilíbrio termodinâmico exige que as suas energias de Fermi sejam iguais. Se as energias de Fermi fossem diferentes, a passagem de um elétron do sólido com maior energia de Fermi para o sólido com menor energia de Fermi resultaria em uma diminuição da energia total do sistema e o sistema composto não estaria, então, em sua configuração de equilíbrio, a de mínima energia, conforme exigido pelas leis da termodinâmica. Este fato dá origem a um fenômeno conhecido por diferença de potencial de contato que encontra diversas aplicações práticas, a saber na eletrônica de estado sólido (junção PN) e no uso do metal de sacrifício em navios.

Ilustração do conceito para compartimento monodimensional quadrado

A monodimensional compartimento quadrado infinito é um modelo para uma caixa mono dimensional. É um sitema modelo padrão em mecânica quântica para o qual a solução para uma partícula isolada é bem conhecido. Os níveis são marcados por um único número quântico n e as energias são dadas por

${\displaystyle E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\,}$.

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Suponha-se agora que em vez de uma partícula nesta caixa nós temos N partículas na caixa e que estas partículas são férmions com spin 1/2. Então somente duas partículas podem ter a mesma energia i.e. duas partículas podem ter a energia de ${\displaystyle E_{1}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}}$,

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 ou duas partículas podem ter energia ${\displaystyle E_{2}=4E_{1}}$ e assim por diante. A razão que duas partículas podem ter a mesma energia é que uma partícula de spin 1/2 pode ter um spin de 1/2 (spin "acima") ou um spin de -1/2 (spin "abaixo"), conduzindo a dois estadois para cada nível de energia. Quando nós olhamos na energia total deste sistema, a configuração para as quais a energia total é a menor (o estado fundamental), é a configuração onde todos os níveis de energia acima de n=N/2 estão ocupados e todos os níveis mais altos estão vazios. A energia de Fermi é consequentemente

${\displaystyle E_{f}=E_{N/2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}(N/2)^{2}\,}$.

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O caso tridimensional

O caso tridimensional isotrópico é conhecido como a esfera de Fermi.

Deixe-nos agora considerar uma caixa cúbica tridimensional que tem um lado de comprimento L (ver compartimento quadrado infinito). Este torna-se uma muito boa aproximação para descrever elétrons em um metal.

Os estados agora são marcados po três números quânticos n_x, n_y, e n_z. As energias da partícula isolada são

${\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

n_x, n_y, n_z são inteiros positivos.

Existem múltiplos estados com a mesma energia, por exemplo ${\displaystyle E_{100}=E_{010}=E_{001}}$. Agora deixemos colocar-se N férmions não interativos de spin 1/2 nesta caixa. Para calcular a energia de Fermi, nós veremos no caso de que N é grande.

Se nós introduzios um vetor ${\displaystyle {\vec {n}}=\{n_{x},n_{y},n_{z}\}}$ então cada estado quântico corresponde a um ponto num "n-espaço" com energia

${\displaystyle E_{\vec {n}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|{\vec {n}}|^{2}\,}$.

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O número de estados com energia menor que E_f é igual ao número de estados que residem em uma esfera de raio ${\displaystyle |{\vec {n}}_{f}|}$ na região do "n-espaço" onde n_x, n_y, n_z são positivos. No estado básico este número iguala o número de férmions no sistema.

${\displaystyle N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{f}^{3}\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Os três férmions que ocupam os mais baixos estados de energia formam uma esfera em espaço de momento. A superfície desta esfera é a superfície de Fermi.

o fator é de dois é novamente porque são doisestados de spin, o fator de 1/8 é porque somente 1/8 da esfera repousa na região onde todos n são positivos.

Nós obtemos

${\displaystyle n_{f}=\left({\frac {3N}{\pi }}\right)^{1/3}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

então a energia de Fermi é dada por

${\displaystyle E_{f}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{f}^{2}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle ={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Tais resultados em uma relação entre a energia de Fermi e o número de partículas por volume (quando nós substituímos L² com V^2/3):

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}\,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A energia de Fermi total de um esfera de fermi de ${\displaystyle N_{0}}$ férmions é dada por

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={3 \over 5}N_{0}E_{f}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={\int _{0}}^{N_{0}}{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{\frac {2}{3}}dN}$

${\displaystyle ={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}{\int _{0}}^{N_{0}}N^{\frac {2}{3}}dN={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}\left({\frac {3}{5}}N_{0}^{\frac {5}{3}}\right)={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Energia de Fermi total:

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Integração por substituição:

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}={\frac {3}{5}}N_{0}\left[{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N_{0}}{\pi }}\right)^{2/3}\right]={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A eliminação de ${\displaystyle L}$ em favor de ${\displaystyle V}$:

${\displaystyle L^{2}=V^{\frac {2}{3}}}$

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}N_{0}^{\frac {5}{3}}}{10mV_{0}^{\frac {2}{3}}}}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Energias de Fermi típicas

Anãs brancas

Estrelas conhecidas como anãs brancas tem massa comparável a nosso Sol, mas têm um raio aproximadamente 100 vezes menor. As alta densidades implicam que os elétrons estão não mais ligados a um núcleo isolado e formam um gás de elétrons degenerado. Os números da densidade de elétrons em uma anã branca são da ordem de 10³⁶ elétrons/m³. Isto significa que sua energia de Fermi é:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} \,}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Núcleos

Outro exemplo típico é as partículas em um núcleo de um átomo. Os núcleons de um núcleo atômico pode ser tratado, assim, como um gás de Fermi e como tal, modelado.^[2]

O raio do núcleo é aproximadamente^[3]:

${\displaystyle R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde A é o número de núcleons.

O número densidade de núcleons em um núcleo é conseqüentemente:

${\displaystyle n={\frac {A}{{\begin{matrix}{\frac {4}{3}}\end{matrix}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m} ^{-3}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Agora, como a energia de fermi somente aplica-se a férmions de mesmo tipo, deve-se dividir esta energia por dois. Isto por causa da presença de nêutrons que não afetam a energia de Fermi dos prótons no núcleo, e vice versa.^[4][5][6]

Assim a energia de fermi de um núcleo é dada por:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{p}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 30\times 10^{6}\ \mathrm {eV} =30\ \mathrm {MeV} }$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O raio do núcleo admite desvios em torno do valor mencionado acima, então um típico valor para a energia de Fermi normalmente dada é 38 MeV.

Um gás de férmions, gás de Fermi ou gás de elétrons livres é um conjunto de férmions não interativos. É a versão na Mecânica Quântica de um gás ideal, para o caso de partículas fermiônicas. Elétrons em metais e semicondutores e nêutrons em estrelas de nêutrons podem aproximadamente ser considerados gases de Fermi.

A distribuição de energia dos férmions em um gás de Fermi em equilíbrio térmico é determinada por sua densidade, pela temperatura e pelos estados de energia disponíveis, via a estatística de Fermi-Dirac. Pelo princípio de exclusão de Pauli, nenhum estado quântico pode ser ocupado por mais que um férmion, então a energia total do gás de Fermi à temperatura do zero absoluto é tão grande quanto o produto do número de partículas pelo estado de energia de cada partícula. Por esta razão, a pressão de um gás Fermi é diferente de zero na temperatura de zero absoluto, em contraste com um gás ideal clássico. Esta então chamada pressão de degenerescência estabiliza uma estrela de nêutrons (um gás de Fermi de nêutrons) ou uma estrela anã branca (um gás de Fermi de elétrons) contra a tração interna da gravidade.

É possível definir uma temperatura de Fermi abaixo do qual o gás pode ser considerado degenerado. Esta temperatura depende da massa dos férmions e da energia da densidade dos estados. Para metais, a temperatura do gás de elétrons de Fermi é geralmente de muitos milhares de kelvins, quando então eles podem ser considerados degenerados. A máxima energia dos férmions a temperatura do zero absoluto é chamada energia de Fermi. A superfície da energia de Fermi no momento espacial é chamada superfície de Fermi.

Desde que as interações são negligenciadas por definição, o problema de tratar propriedades do equilíbrio e o comportamento dinâmico de um gás de Fermi se reduz ao estudo do comportamento de partículas independentes e isoladas. Como está, é ainda relativamente tratável e dá forma ao ponto de servir de base para teorias mais avançadas (tais como a teoria do líquido de Fermi ou a teoria perturbacional) as quais levam em conta as interações com algum grau de exatidão.

Índice

• 1Descrição matemática
• 2Gás de Fermi como modelo para os núcleos dos átomos
• 3Referências
• 4Ver também
• 5Ligações externas

Descrição matemática

Dentro da estrutura que a física estatística possibilita, segue-se que com a ajuda de conjuntos estatísticos para um número médio de ocupação ${\displaystyle \langle n_{i}\rangle }$ dos estados ${\displaystyle |i\rangle }$ com a energia ${\displaystyle E_{i}}$ da estatística de Fermi-Dirac:

${\displaystyle \langle n_{i}\rangle ={\frac {1}{e^{\frac {E_{i}-\mu }{k_{B}T}}+1}}}$

/////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde ${\displaystyle \mu }$ é o potencial químico, ${\displaystyle T}$ a temperatura e ${\displaystyle k_{B}}$ a constante de Boltzmann.

Estes férmions, que estão sujeitos ao princípio de exclusão de Pauli, podem estar na condição de máxima ocupação, ou seja ${\displaystyle \langle n_{i}\rangle \leq 1}$. Esta condição é que a estatística de Fermi-Dirac tratará para qualquer valor de preenchimento pleno ${\displaystyle \mu }$, porque o potencial químico de um gás ideal de Fermi não é sujeito a quaisquer restrições.